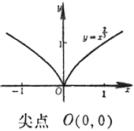
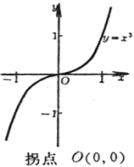
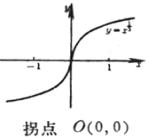
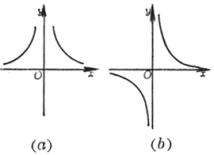
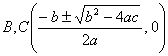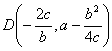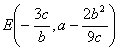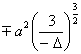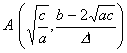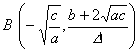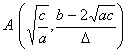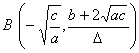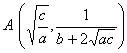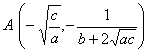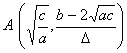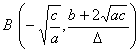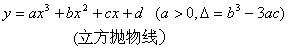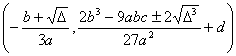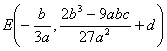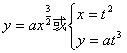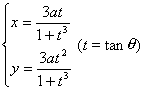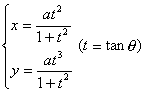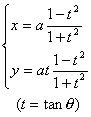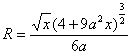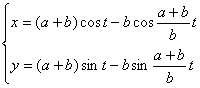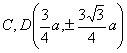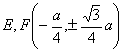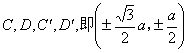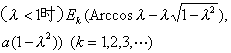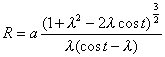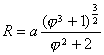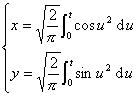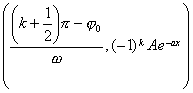§8 重要平面曲线表
[三次曲线]
|
方 程 与 图 形 |
特 征 |
|
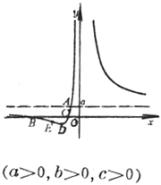
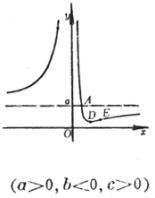
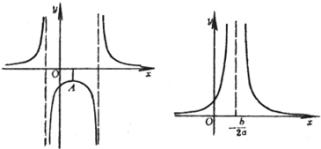
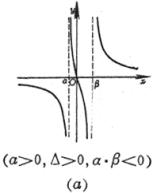
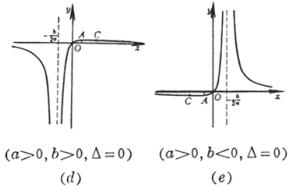
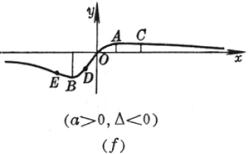
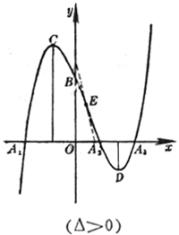
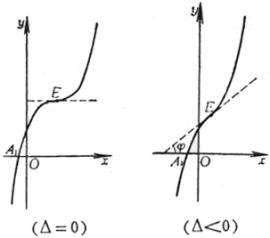
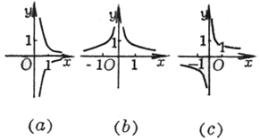
(a >0 , b<0 ,Δ>0) (a >0 , b<0 ,Δ=0) (a) (b)
这些曲线都是关于直线 |
曲线由两支组成 渐近线y = a与x = 0 曲线与y = a的交点
曲线与x轴的交点
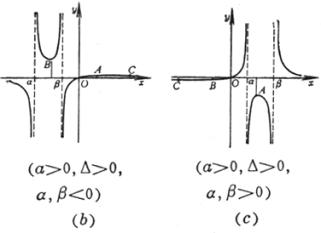
极值点 拐 点 ( a ) 不连续点 极 大 点 渐 近 线 (b) 不连续点 渐 近 线
(c) 极 大 点
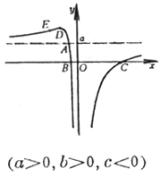
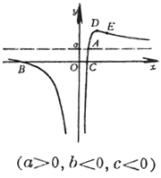
拐 点 在这两点的斜率分别为 渐 近 线 y = 0 |
|
方 程 与 图 形 |
特 征 |
|
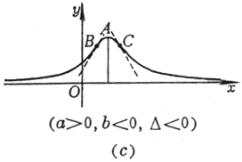
[注] a, b为方程 |
(a) 不连续点 x = a,x = b 渐 近 线 y = 0和x = a,x = b (b) 不连续点 x = a,x = b 极 大 点
极 小 点 拐 点 C 渐 近 线 y = 0和x = a,x = b ( c ) 不连续点 x = a,x = b 极 大 点
极 小 点 拐 点 C 渐 近 线 y = 0和x = a,x = b (d) 不连续点 极 大 点
拐 点 C 渐 近 线
y = 0和 (e) 不连续点 极 小 点 拐 点 C 渐 近 线
y = 0和 (f) 极 大 点
极 小 点 拐 点 C, D, E三点 渐 近 线 y = 0 |
上述三次曲线的图形,只列出a>0的情况,对于a<0时,除曲线![]() (当a>0时渐近线在x轴上方,当a<0时,渐近线在x轴下方)外,一般作适当变化后,与a>0时的曲线都是关于x轴对称的.例如a<0时,两条曲线:
(当a>0时渐近线在x轴上方,当a<0时,渐近线在x轴下方)外,一般作适当变化后,与a>0时的曲线都是关于x轴对称的.例如a<0时,两条曲线:![]() 与
与![]() 是关于x轴对称的,而后者x2系数
是关于x轴对称的,而后者x2系数![]() .
.
[抛物型曲线]
|
方 程 与 图 形 |
特 征 |
|
|
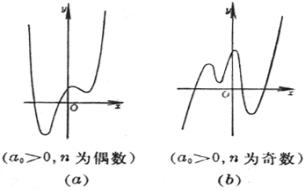
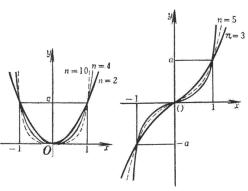
(a) y由 极值点 奇数个(1~n-1) 拐 点 偶数个(0~n-2) (b) y由 极值点 偶数个(0~n-1) 拐 点 奇数个(1~n-2) 曲线与x轴的交点A1,
A2,A3(或一个交点A1)为方程 极值点 拐 点
的对称中心,该点的切线斜率为 |
|
方 程 与 图 形 |
特 征 |
|
(a) (b) |
(a)
顶点(同极值点)O(0, 0) 曲线关于y轴对称 (b)
拐点 O(0, 0) 曲线关于原点对称 |
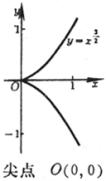
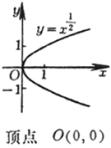
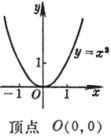
![]() (m, n为两个互素的整数)
(m, n为两个互素的整数)
![]()
|
n为偶数 m奇数 |
n为奇数 m偶数 |
n为奇数 m奇数 |
相切情况 |
|
|
m>n m<n 对称情况 |
关于x轴对称 |
关于y轴对称 |
关于原点对称 |
在原点处与x轴相切 在原点处与y轴相切 |
|
方 程 与 图 形 |
特 征 |
|
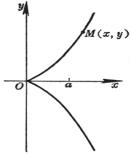
[双曲型曲线]
[半立方抛物线]
[箕舌线]
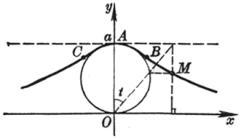
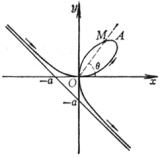
[笛卡儿叶形线]
或
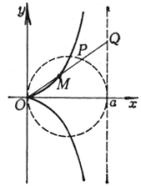
[蔓叶线]
或 或 [环索线]
或 或 [尼哥米德蚌线]
或 或
|
(a) n为偶数: 不连续点 O(0, 0) 渐 近 线 y = 0与x = 0 曲线关于y轴对称 (b) n为奇数: 曲线关于原点对称 (a) 不连续点 O(0, 0) 渐 近 线 y = 0与x = 0 曲线关于x对称 (b) 曲线关于y对称 (c) 曲线关于原点对称 尖点
曲率半径 弧长
极大点 拐 点
渐 近 线
曲线与渐近线之间的面积 结 点
顶 点
渐近线 圈套所围成的面积 曲线与渐近线之间的面积 曲线是使 尖 点
渐近线 曲线与渐近线之间的面积 曲线是使PM1 = PM2 = OP的点M1 , M2的轨迹(P为y轴上一点,M1,M2在过A, P两点的射线上) 顶 点 A(a, 0) 结 点 O(0, 0) 渐近线 x = -a 圈套所围成的面积
曲线与渐近线之间的面积
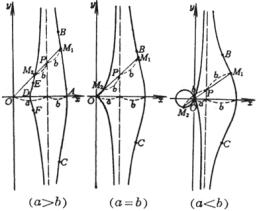
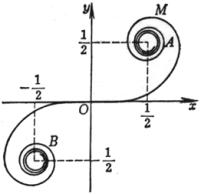
曲线是使OM1 = OP + b,OM2 = OP - b的点M1,M2的轨迹(分别称为外支线(右)和内支线(左)) 外支线 顶 点 A(a + b, 0) 拐 点 B, C,它们的横坐标等于方程x3 – 3a2x + 2a(a2 – b2) = 0的最大根 内支线 顶 点 D(a - b, 0) 拐 点(a>b时)E, F,它们的横坐标等于方程x3 – 3a2x + 2a(a2 – b2) = 0的第二个正根 尖 点(a=b时) O(0, 0) 结 点(a<b时) O(0, 0) 内外支线的渐近线x = a |
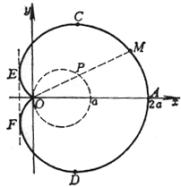
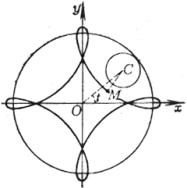
[帕斯卡蜗线]
![]()
或
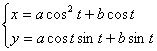
或
![]() (
(![]() 为圆的直径)
为圆的直径)
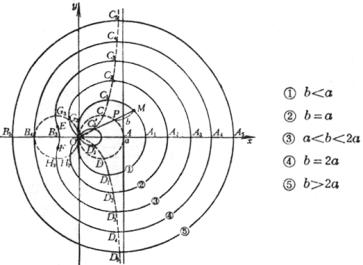
曲线是使OM = OP ± b的点M的轨迹(P点在直径为a的圆周上)
顶 点 Ak, Bk(a ± b, 0)(k=1, 2, 3, 4, 5),B2与原点重合
结 点(b<a时)O(0, 0),在该点的切线的斜率为![]() ,该点的曲率半径为
,该点的曲率半径为![]()
尖 点(b=a时)O(0, 0)
孤立点(b>a时)O(0, 0)
极值点
当b<a时有4个,当b³a时有2个: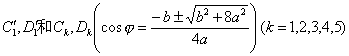 当b从0变到¥时,所有极值点构成蔓叶线
当b从0变到¥时,所有极值点构成蔓叶线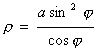
拐点(a<b<2a时)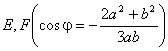
二重切线的切点(b<2a时):
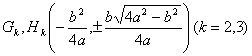
这些切点在圆r = - acosj上蜗线所围成的面积
![]()
(当b<a时,内圆的面积计算了两次)
[注] 当b=a时,即为心脏线.
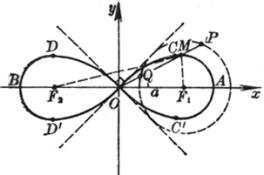
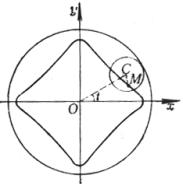
[卡西尼卵形线]
![]()
或![]()
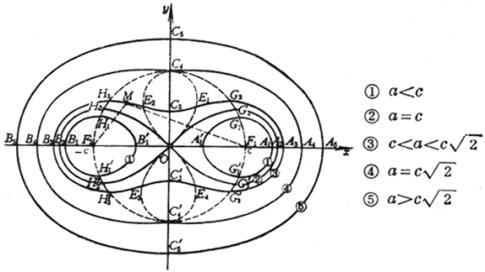
曲线是使MF1×MF2 = a2的点M的轨迹(F1, F2为固定焦点,F1F2 = 2c,a为常数).
顶 点 ![]()
![]()
极值点 ![]()
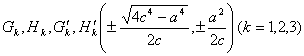
或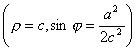
当a从0变到![]() 时,所有极值点构成一个圆(半径为c)
时,所有极值点构成一个圆(半径为c)
拐 点 ![]()
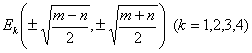
其中
![]()
或
![]()
当a从c变到![]() 时,所有拐点构成双纽线
时,所有拐点构成双纽线
[注]当a=c时,即为双纽线.
|
[心脏线] 或 或 [双纽线] 或
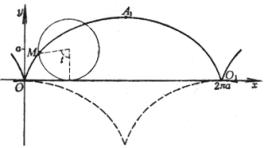
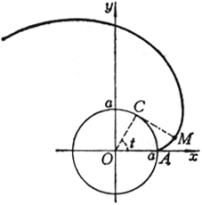
[普通旋轮线(摆线)] 或
[长(或短)辐旋轮线(次摆线)]
长轴(λ>1)
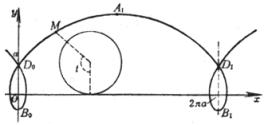
短轴(λ<1) [圆外旋轮线(外摆线)]
(a为定圆的半径,b为动圆的半径,t = ÐCOx) |
(i) 它是使OM = OP ± a的点M的轨迹(a为圆的直径,P为圆周上的一点) (ii) 它是圆外旋轮线的特例(动圆与定圆的直径相等) 尖 点 O(0, 0) 顶 点 A(2a, 0) 极值点 二重切线的切点
曲线长 L = 8a 面 积 (i) 它是使MF1 × MF2 = a2的点M的轨迹(OF1 = a) (ii)
它是使OM = PQ的点M的轨迹(P, Q在圆心为F1,半径为 结 点 (同拐点)O(0, 0),在该点的切线的斜率为± 1 顶 点 极值点 曲率半径 双纽面积 S = 2a2 曲线是一圆周沿x轴滚动而无滑动时,圆周上一点M所描成的轨迹(圆的半径为a) 周 期 T = 2pa 极值点
曲率半径 渐屈线 为一旋轮线(图中虚线) 拱 长 面 积 曲线是一圆周沿x轴滚动而无滑动对,圆外一点M(或圆内一点N)所描成的轨迹(圆的半径为a) 周 期 T = 2pa 结 点
拐 点 极大值点
极小值点 曲率半径
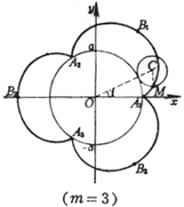
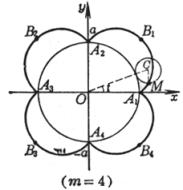
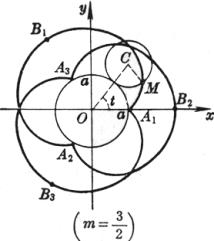
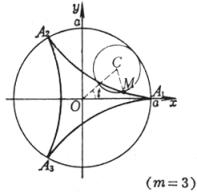
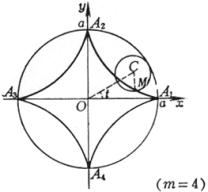
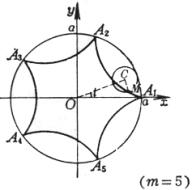
对应于极值点(l<1时)处的曲率半径为 曲线是一圆周沿另一圆周外部滚动而无滑动时,圆周上一点M所描成的轨迹,曲线的形状由 (i) 当m = 1时,曲线是心脏线 (ii) 当m为整数时,曲线由m支组成,动点M描完m支后(即动圆绕定圆一周),返回起始位置 (iii)
当m为分数( (iv) 当m为无理数时,有无穷多的分支,动点M不能返回起始位置 尖 点 顶 点
曲线长(一支) 曲率半径 扇形A1B1A2A1的面积(不包括定圆的面积) |
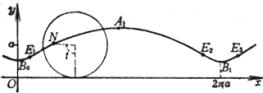
[圆内旋轮线(内摆线)]
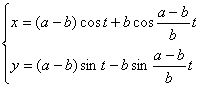
(a为定圆半径,b为动圆半径,t = ÐCOx)
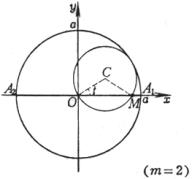
曲线是一圆周沿另一圆周的内部滚动而无滑动时,圆周上一点M所描成的轨迹.
圆内旋轮线的尖点、顶点的坐标,弧长,曲率半径及面积公式都与圆外旋轮线一样,只须把“+b”换成“-b”.![]() 总是大于1,特别,当m = 4时,曲线有4只,称为星形线,其方程为
总是大于1,特别,当m = 4时,曲线有4只,称为星形线,其方程为
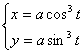 或
或![]()
全曲线长L = 6a
曲线所围成的面积 ![]()
[长(或短)辐圆外旋轮线(外次摆线)]
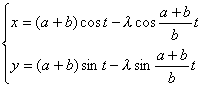 (a为定圆半径,b为动圆半径)
(a为定圆半径,b为动圆半径)
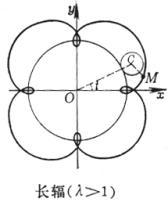
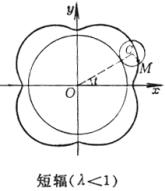
曲线是一圆周沿另一圆周的外部滚动而无滑动时,圆周外部(或内部)一点M所描成的轨迹.
[长(或短)辐圆内旋轮线(内次摆线)]
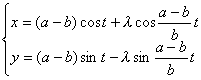 (a为定圆半径,b为动圆半径)
(a为定圆半径,b为动圆半径)
长辐![]() 短辐
短辐![]()
曲线是一圆周沿另一圆周的内部滚动而无滑动时,圆周外部(或内部)一点M所描成的轨迹.特别,当a=2b时,长短辐圆内旋轮线是一个椭圆;当a=b时,是帕斯卡蜗线.
|
方 程 与 图 形 |
特 征 |
|
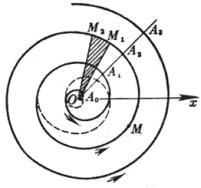
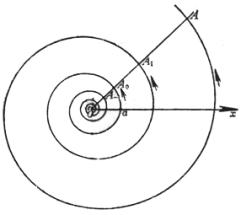
[阿基米德螺线]
|
曲线为一动点以常速 (方程 等距性 过极点的射线与曲线交于A0,A1,A2,L,它们是等间隔( 弧 长 曲率半径 扇形M1OM2的面积 |
|
[对数螺线(等角螺线)]
|
曲线与所有过极点的射线的交角都相等(a)(k=cota),当 等比性 过极点的射线与曲线交于L,A-1,A0,A1,L,则L, 弧长 曲率半径 [注]当 |
[双曲螺线(反螺线)]
![]()
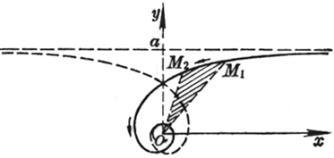
渐近点 极点O(当![]() 时)
时)
渐近线 y=a
曲率半径 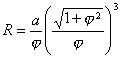
扇形M1OM2的面积 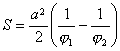
曲线由两支组成,它们关于y轴对称
[连锁螺线]
![]()
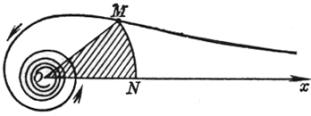
曲线是当N在x轴上移动时,使圆扇形OMN的面积保持一定![]() 的点M的轨迹
的点M的轨迹
渐近点 极点O(当![]() 时)
时)
渐近线 x轴(当![]() 时)
时)
|
方 程 与 图 形 |
特 征 |
|
[圆的渐开线] |
尖点 A(a,,0) 与x轴的交点 B( (式中t0为方程t=tant的根) 弧长 曲率半径 曲率中心C在圆周上 曲线由两支组成,它们关于x轴对称 |
|
[回旋曲线] |
拐点 O(0,0) 渐近点 A( B( 弧长 曲线关于原点对称 |
|
方 程 与 图 形 |
特 征 |
|
[悬链线] |
顶点 A(0, a) 弧长 曲边梯形OAMP的面积 曲率半径 曲线关于y轴对称,位于抛物线y=a+ [注] 把一条柔软而不能伸长的重绳悬挂于 两点,便得到悬链线的形状 |
|
[曳物线] x=aArch 或 x=aln |
尖点 A(0,a),在该点与y轴相切 弧长 曲率半径 R=acot 曲线关于y轴对称,是悬链线的渐开线,从顶点A开始展开,这一曲线的切线与x轴的交点到切点的距离为一常数. [注] 把长度为a的柔软而不能伸长的绳子的 一端系一质点M,另一端P沿轴x移动, 则点M便描成曳物线形状 |
[玫瑰线]![]()
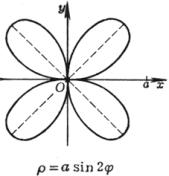
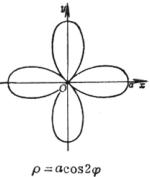
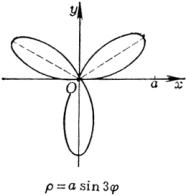
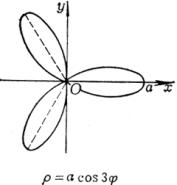
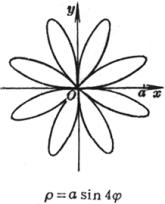
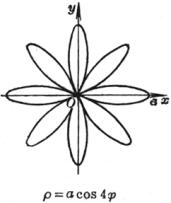
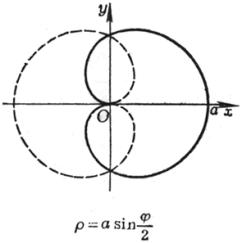
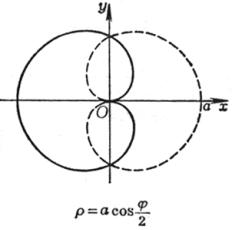
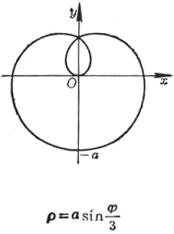
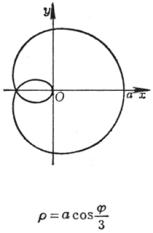
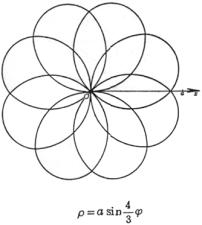
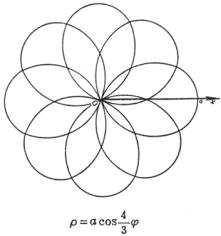
|
方 程 与 图 形 |
特 征 |
|
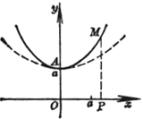
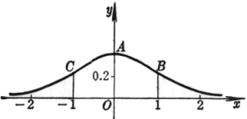
[概率曲线] y=a
|
顶点(同极大点) A(0, a) 拐点 B,C 该点切线的斜率为 曲线与x轴间的面积 曲线关于y轴对称 |
|
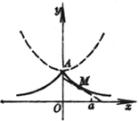
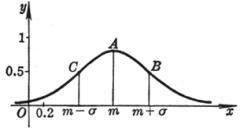
[标准正态分布曲线(高斯曲线)] y=
|
顶点 A(0, 拐点 B,C( 曲线与x轴间的面积为1 曲线关于y轴对称 |
|
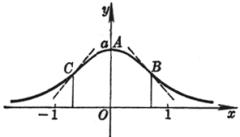
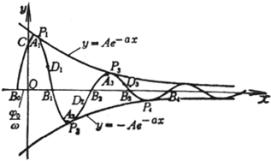
[一般正态分布曲线] y= [阻尼振动曲线] y=A
|
顶点(同极大点) A(m, 拐点 B,C(m 曲线与x轴间的面积为1 曲线关于直线x=m对称 与x轴的交点 Bk 与y轴的交点C(0,Asin 极值点 Ak的横坐标为 拐点 Dk的横坐标为 曲线与两条指数曲线 y= Pk |