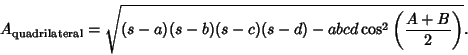The semiperimeter on a figure is defined as
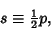 |
(1) |
where 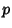 is the Perimeter. The semiperimeter of Polygons appears in unexpected ways in the
computation of their Areas. The most notable cases are in the Altitude, Exradius, and
Inradius of a Triangle, the Soddy Circles, Heron's Formula for the Area of a
Triangle in terms of the legs
is the Perimeter. The semiperimeter of Polygons appears in unexpected ways in the
computation of their Areas. The most notable cases are in the Altitude, Exradius, and
Inradius of a Triangle, the Soddy Circles, Heron's Formula for the Area of a
Triangle in terms of the legs 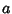 ,
, 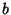 , and
, and 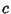
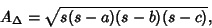 |
(2) |
and Brahmagupta's Formula for the Area of a Quadrilateral
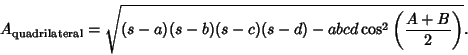 |
(3) |
The semiperimeter also appears in the beautiful L'Huilier's Theorem about Spherical Triangles.
For a Triangle, the following identities hold,
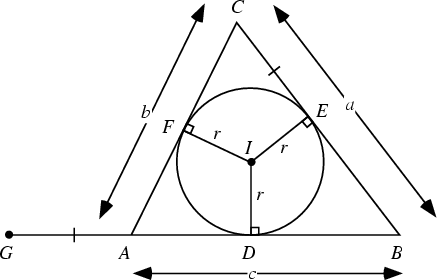
Now consider the above figure. Let 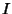 be the Incenter of the Triangle
be the Incenter of the Triangle
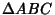 , with
, with 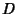 ,
, 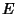 , and
, and 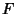 the tangent points of the Incircle.
Extend the line
the tangent points of the Incircle.
Extend the line 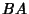 with
with 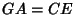 . Note that the pairs of
triangles
. Note that the pairs of
triangles 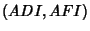 ,
, 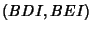 ,
, 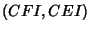 are congruent. Then
are congruent. Then
Furthermore,
(Dunham 1990). These equations are some of the building blocks of Heron's  derivation of
Heron's Formula.
derivation of
Heron's Formula.
References
Dunham, W. ``Heron's Formula for Triangular Area.'' Ch. 5 in
Journey Through Genius: The Great Theorems of Mathematics. New York: Wiley, pp. 113-132, 1990.
© 1996-9 Eric W. Weisstein
1999-05-26