Let a linear system of equations be denoted
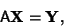 |
(1) |
where
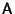 is a Matrix and X and Y are Vectors. As shown by Cramer's Rule,
there is a unique solution if
is a Matrix and X and Y are Vectors. As shown by Cramer's Rule,
there is a unique solution if
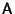 has a Matrix Inverse
has a Matrix Inverse
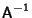 . In this case,
. In this case,
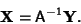 |
(2) |
If
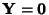 , then the solution is
, then the solution is
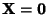 . If
. If
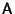 has no Matrix Inverse, then the solution
Subspace is either a Line or the Empty Set. If two equations are multiples of each other, solutions
are of the form
has no Matrix Inverse, then the solution
Subspace is either a Line or the Empty Set. If two equations are multiples of each other, solutions
are of the form
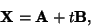 |
(3) |
for 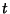 a Real Number.
a Real Number.
See also Cramer's Rule, Matrix Inverse
© 1996-9 Eric W. Weisstein
1999-05-26