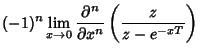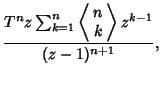The 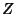 -transform of
-transform of 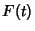 is defined by
is defined by
![\begin{displaymath}
Z[F(t)]={\mathcal L}[F^*(t)],
\end{displaymath}](z_29.gif) |
(1) |
where
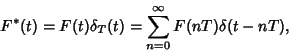 |
(2) |
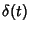 is the Delta Function,
is the Delta Function,
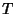 is the sampling period, and
is the sampling period, and 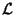 is the Laplace Transform. An alternative definition is
is the Laplace Transform. An alternative definition is
![\begin{displaymath}
Z[F(t)]=\sum_{\rm residues} \left({1\over 1-e^{Tz}z^{-1}}\right)f(z),
\end{displaymath}](z_34.gif) |
(3) |
where
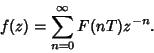 |
(4) |
The inverse 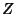 -transform is
-transform is
![\begin{displaymath}
Z^{-1}[f(z)]=F^*(t)={1\over 2\pi i}\oint f(z)z^{n-1}\,dz.
\end{displaymath}](z_36.gif) |
(5) |
It satisfies
![$\displaystyle Z[aF(t)+bG(t)]$](z_37.gif) |
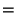 |
![$\displaystyle a Z[F(t)]+b Z[F(t)]$](z_39.gif) |
(6) |
![$\displaystyle Z[F(t+T)]$](z_40.gif) |
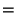 |
![$\displaystyle z Z[F(t)]-zF(0)$](z_41.gif) |
(7) |
![$\displaystyle Z[F(t+2T)]$](z_42.gif) |
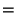 |
![$\displaystyle z^2 Z[F(t)]-z^2 F(0)-z F(t)$](z_43.gif) |
(8) |
![$\displaystyle Z[F(t+mT)]$](z_44.gif) |
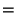 |
![$\displaystyle z^m Z[F(t)]-\sum_{r=0}^{m-1} z^{m-r}F(rt)$](z_45.gif) |
(9) |
![$\displaystyle Z[F(t-mT)]$](z_46.gif) |
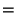 |
![$\displaystyle z^{-m}Z[F(t)]$](z_47.gif) |
(10) |
![$\displaystyle Z[e^{at}F(t)]$](z_48.gif) |
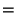 |
![$\displaystyle Z[e^{-aT}z]$](z_49.gif) |
(11) |
![$\displaystyle Z[e^{-at}F(t)]$](z_50.gif) |
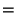 |
![$\displaystyle Z[e^{aT}z]$](z_51.gif) |
(12) |
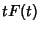 |
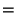 |
![$\displaystyle -Tz{d\over dz} Z[F(t)]$](z_53.gif) |
(13) |
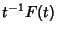 |
 |
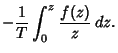 |
(14) |
Transforms of special functions (Beyer 1987, pp. 426-427) include
![$\displaystyle Z[\delta(t)]$](z_56.gif) |
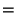 |
 |
(15) |
![$\displaystyle Z[\delta(t-mT)]$](z_58.gif) |
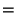 |
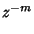 |
(16) |
![$\displaystyle Z[H(t)]$](z_60.gif) |
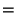 |
 |
(17) |
![$\displaystyle Z[H(t-mT)]$](z_62.gif) |
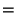 |
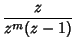 |
(18) |
![$\displaystyle Z[t]$](z_64.gif) |
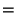 |
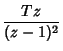 |
(19) |
![$\displaystyle Z[t^2]$](z_66.gif) |
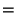 |
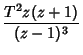 |
(20) |
![$\displaystyle Z[t^3]$](z_68.gif) |
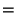 |
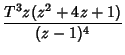 |
(21) |
![$\displaystyle Z[a^{\omega t}]$](z_70.gif) |
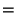 |
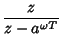 |
(22) |
![$\displaystyle Z[\cos(\omega t)]$](z_72.gif) |
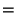 |
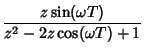 |
(23) |
![$\displaystyle Z[\sin(\omega t)]$](z_74.gif) |
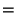 |
![$\displaystyle {z[z-\cos(\omega T)]\over z^2-2z\cos(\omega T)+1},$](z_75.gif) |
(24) |
where 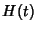 is the Heaviside Step Function. In general,
is the Heaviside Step Function. In general,
where the
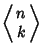 are Eulerian Numbers. Amazingly, the
Z-transforms of
are Eulerian Numbers. Amazingly, the
Z-transforms of 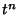 are therefore generators for Euler's Triangle.
are therefore generators for Euler's Triangle.
See also Euler's Triangle, Eulerian Number
References
Beyer, W. H. (Ed.). CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, pp. 424-428, 1987.
Bracewell, R. The Fourier Transform and Its Applications. New York: McGraw-Hill, pp. 257-262, 1965.
© 1996-9 Eric W. Weisstein
1999-05-26
![]() -transform of
-transform of ![]() is defined by
is defined by
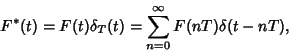
![\begin{displaymath}
Z[F(t)]=\sum_{\rm residues} \left({1\over 1-e^{Tz}z^{-1}}\right)f(z),
\end{displaymath}](z_34.gif)
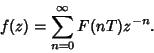
![$\displaystyle z^m Z[F(t)]-\sum_{r=0}^{m-1} z^{m-r}F(rt)$](z_45.gif)
![$\displaystyle -Tz{d\over dz} Z[F(t)]$](z_53.gif)
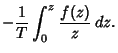
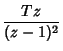
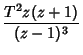
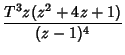
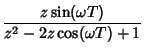
![$\displaystyle {z[z-\cos(\omega T)]\over z^2-2z\cos(\omega T)+1},$](z_75.gif)